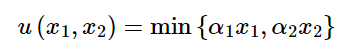
こういうのだけど、x1をα2消費して、x2をα1消費したら、効用α1α2を得るのはわかると思います。ここからx1を増やしたり、x2を増やしたりしても効用は変わらないので、必ず「x1をα2消費して、x2をα1消費して」というバスケットで消費量を増やしていかないと効用増にならないよね。

ただこれだと効用一単位が効用α1α2だから、バスケットだと言った「x1をα2消費して、x2をα1消費して」は、割り算して、「x1を1/α1消費して、x2を1/α2消費して」にすると効用一単位が効用1になる

u(x,y,z) = min{x+y, z}

みたいな問題が以前横国で出たと思ったけど、これはx1=x+y, x2=z, α1=α2=1だね。

x,y,z の価格を px,py,pzとして、

px＞py ならば最適消費において x=0、y=z、予算制約式を (py + pz) 2y = I と書けるね。

px＜py ならば最適消費において y=0、x=z、予算制約式を (px + pz) 2x = I と書けるね。

px＝py ならば最適消費において x+y = z、予算制約式を (px + pz) 2z = I と書けるね。

偉そうにこういうことを言うと、レオンチェフ型効用関数で描かれる二財は完全補完財で、追加効用一単位のために必ずバスケットで消費しないといけないから単一の財の需要関数に複数財の価格が消えないんじゃないかな？ウフフ