世界史を今さら勉強したくないひとで、経済史を勉強しようにも「そんなの常識」みたいに思われている要素からして頭にないせいで苦痛苦行だと言う人もいるはずです。上記の『図解雑学 横割り世界史』は大変おすすめな一冊となっております。決してアホではないのに、いまいち高等学校で世界史を勉強したくならなかった時点で、君が望んでいる世界史の参考書は十中八九、こういうのだと思います。一旦エジプトや地中海方面の話をしてから、また時間がいくらか巻き戻って別の地域の学習が始まるとき、その時点で苦痛なんだと思います。
実際、経済史、世界経済史の勉強をするにあたって要点になってくるのは、植民地主義、産業革命、帝国主義時代、冷戦など、全球的なムーブメントが狙われている気がしますね。横割りのほうが、経済史前提なら今更苦にならなくていいと思います。
関数がわからないひとは、そもそも二つの量が伴って変化するという現象が理解できない。お風呂のお湯を入れっぱなしにすると溜まりますが、お湯を入れた時間と溜まった量は伴って変化します。
はい！アウトーーー！！！
たぶんいまついてこれなかったと思う。なんでそんな言い方をするんですかと思ったと思う。一言、「増える」って言えばいいじゃないですかと思ったと思いますが、数学（関数）というのはとどのつまりそのあたりの配慮が徹底的に欠落した学問領域なんですよ。お湯を入れた時間と溜まった量は伴って「増える」んじゃなくて「変化する」んだお！
これが怖いか？
おんなじだお！もはや日本語で書いてもらえないんだお。伴って変化する二つがあるといきなりこういう記号を読まされる。これは「 t がほんの少し増えたとき、f がその何倍増えるか」です。こちらの記号で書かれている場合は、ｔがほんの少し増えたとき、数式上明確になっているｆの増分だけでなく、たとえばｔが増えたせいでｘもいくらか増えていて、ｘがいくらか増えたせいでｆがいくらか増えるぶんも全部計上してあげないといけません。
これも「ｔがほんの少し増えたとき、ｆがその何倍増えるか」ですが、こちらはｔがほんの少し増えたとき、数式上明確になっているｆの増分だけで構いません。
電車が駅に到着して出入口がプシャーッ！て開いたとします。するといままでホームにいた人たちが複数ある出入口のどこかに吸い込まれていくと思います。たとえば筆者が a1 という位置にいたとして、一番近い出入口が a だとしたら。一歩二歩、体を揺するように出入口に近づいて行って、たとえば、
a1 → a2 → a3 → a4 → a5 → a6 → a7 → a
のように位置が変化していくとします。7歩だったわけですね。これは筆者の位置である点列{ai}が aに収束したことを意味します。ちなみに右から近づいても、左から近づいても同じ出入口ならば同じ位置に収束します。
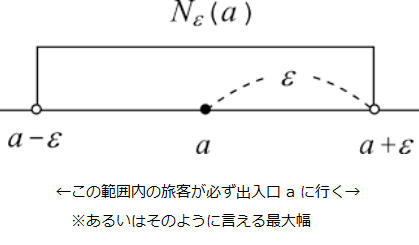
Nε(a)が定義された近傍。aは出入口。a-εはaに必ず吸い込まれる位置の左端、a+εは右端。
数学の「近傍」とは、「ある特定の点の近く」という意味ですが、もしも a の半径 ε 以内であれば必ず点列 {ai} が a に収束するということであれば、そういう意味合いで「近傍」を定義することができますし、その「近傍」にある任意の点は、あるaに収束する点列{ai} が存在して、そこに含まれると言えます。 現実には車内混雑していたりして、ドアの目の前でも諦める場合があるから、このような近傍は定義することは難しいかもしれないですね。
AさんとBさんは、ある同じ船について、川を上ってきて、ある場所で停留している姿を、まったく同じ時刻に見る体験を何度もしてきたという。
Ａさん：船は0.4km地点からスタートして時速0.6キロメートルで川を上ったとしか思えない
Ｂさん：船は0km地点からスタートして時速１キロメールで川を上ったとしか思えない
毎回「1km地点」にあたる場所で停留しているのは間違いないのだろうなと思います。
君たちは中学三年生の頃から、「-2≦x≦4 のとき y の最大値はいくつか？」という問題に対して、x=-2 のときと、x=4 のとき、この二つだけ調べて比べても不正解になったよね。一次関数までだったらどっちか大きいほうだったよね。でも二次関数を習ったあたりから、急に苦手になったよね。
しかし君たちだって、2月の模試で偏差値52で、11月の模試で偏差値52だから、「上手く維持してこれたね。でもここから伸びる受験生は大勢いるよ。」と言われたら嫌だよね、夏休みにうんと頑張って9月の模試でＡ判定だったことを省略されたくないよね。
曲線には概形があるんだけど、概形がわかるというのは「絵的にイメージできました」というわけでは断じてなくて、つまり実際に描画しなくてよくて、早い話が「極値」がいくつあるのかわかればいいんだよね。極値と次の極値の間には、変曲点という名前の付いたスポットがあるにはあるけどそこまで気にしないでよくて、極値と次の極値の間は「増えているか、または減っているか」しかないからな。だから極値と呼ばれるものを左から順に１，２，３，４と番号ふったとして、まあ本当は４つも多くないんだけど、１と２の間は増えてました、２と３の間は減ってました、３と４の間は増えていました、こんな感じなわけです。ここで２と４のどっちの値が高いですか、とか関心事にならないといけない。
第二次導関数の符号を調べる最大の理由。
問題は「極値」だったら「導関数＝０」だけど、「導関数＝０」だったら「極値」ってわけじゃないところな。そっちなんだわ。
陰関数定理とは、たとえば次のような式に出会ったときに
中学生の頃から数学が得意な君たちは「等積変形」をして、y を x の「関数のように書く」ことができるね。でもね、「関数のように書く」という作業が終わったとたん、やっていいとは限らないのが「だからｙは x の関数です」と定義することだよね。関数であるためには、x に対して y が一意に決まらないといけなかったよね。また連続関数だったり、微分可能だったりすることは、どうやって保障されるんだろうな。
そのあたりについて説明しているのが陰関数定理なんだ。どんなとき、等積変形をして遊んでいいか書いてあるんだ。
これはまず左辺をｘとｙの２変数関数としてみたときに、ある特定の点（座標）において、
① x の偏導関数 ② y の偏導関数
がそれぞれ定義できた（左辺が一階微分可能だった）うえで、その特定の点で②≠０を満たし、かつその特定の点の近傍で①②が連続関数であるとき、近傍では「関数のように等積変形した y = φ(x)」は陰関数で微分可能なんだよということ。
まず、はさみうちの原理がなりたたない場合を紹介します。
L’Arc〜en〜Cielさん♪ 途切れない空を何処までも♪影さえも映らない世界へ♪
Glayさん♪ Good-luck 錆びれた影が貴方が♪ジェラシーさえも傷つけた♪最後まで♪
もしもですね、お二方に挟み撃ちされていたとしても何を唄うかわからないわけです。しかしこれが、関数二つだと挟まれている関数の値は予測できる場合があります。そもそも関数二つに挟まれているというのは
任意のxについて、f(x) > h(x) > g(x) がなりたつ
ということです。挟まれている関数がh(x)で、挟んでいる関数がf(x)とg(x)です。ちなみにこれを、関数 f と g が 関数 h を挟んでいるという言い方をされてもひるまないようにね。おんなじだよ。
あとは簡単です。x=0のとき f(0)=g(0)ならば、f(0)=h(0)=g(0)ということですが、これが無限大の極限でもなりたつことがわかっているということです。x→∞で同じ考え方していいんだって。そんなの当たり前だろうという人は、確かに本格的に勉強した人よりも理解が不十分なのですが、そういう会話の流れで「ブッブーッッ！」っていうひとのせいで数学嫌いな人が増えるんだよね。わかればいいですよ。教わったひとが間違えないように教えることのほうが大原則だ。
謝辞：日本代表の皆様おめでとうございます。佐々木朗希投手もおめでとうございます。
筆者は、試合がターニングポイントに差し掛かるほど配球の読みを捕手に外されるレベルの野球フリークだ。インコースとアウトコースの違いがなんとなくわかるから、なんでもないような場面なら次のボールが大体当たる。野球少年時代に、部活のコーチから「ボールの軌道を覚えて、投球を点ではなく線でとらえてごらんなさい。」と教わったものの、インコースは点でとらえるしかなく、アウトコースに行くほど線でとらえやすくなる。バッターボックスの構造上そのようになる。だから速球はインコース、変化球はアウトコースがセオリーになってくる。おそらく初歩の初歩だろう。筆者が捕手をやるとしたら、真ん中高めに外れる剛速球の使い方がいまいちわかっていないなと自分で自分に思う、そんなレベルである。
次のボールの予測が外れ始めると、打者や投手、捕手の顔色やジェスチャーをなんとか読み取ろうとして、いるうちに、一人ひとりの選手をあたかも等身大で考えるようにもなった。心理描写と言うか、人の心理と言えば大学で勉強したことに少し関連あることだ。もしかすると、試合中の選手たち一人ひとりをスタンドで応援しているファンより、等身大で鑑賞したがる少し変わった野球ファンかもしれない。
もちろん野球は見世物だという考え方は嫌いではないし、筆者自身が楽しんで観ている。選手たちへの批判も、本当は温かなものなのだろうなと思う。しかし野球を批判する者が、「所詮見世物だと思っていますね。」とは絶対に受けてはいけない誤解だろうなと思うのである。「楽しくみています、ありがとう。」という感情より大きくなってしまった批判騒動というのは、その辺りを空虚にしてしまうなと思う。技術的なこととして、毎日ケアしている現場の人物の判断は絶対だ、と言うことは、たとえば「野球解説者の自分がこういう発言をしなければならない」のような使命感に駆られても、見落としてはいけないなと思います。そうでないと、「どうして毎日ケアしている人の意見が差し置かれるのですか。」という所から意見が出たりするし、悪くすれば、「差し置いていいから言っているのですよね。」となりかねない。何某か使命感から発言するときは、自分の発言がスタジアムになることまで想定して、慎重に前置きまでできるとエレガントなものだろうなと思う。
佐々木朗希投手はチャプマンみたく代名詞になってほしいです。筆者は、ふざけて、「チャプマン」と言いながらマウンドに登って見せたことがあったのだが、そこが「ささきろうき」とか言いながら、になって欲しいと思う。